Going off on a tangent

Yousuf Marvi and Clara Valtorta

The start of the second Global Math Week is celebrated on 10-10-18. This week has us thinking about joyful, global mathematics, and how mathematics can bring people together from all across the globe. As we mark this week, we can also consider how different mathematics subjects are interconnected to give us exciting ways of exploring similar concepts.

For example, have you ever wondered why we take math classes in a set order? Although the classes seem to cover different skills, often the same phrase or concept appears across multiple subjects. For example, the word tangent shows up in algebra, geometry, and calculus. Then, have you ever wondered how this concept is connected across these math courses? Is the concept of tangent different in each one?

Let’s explore how a tangent line interacts with a circle. A tangent line of a circle is a line that passes through exactly one point on the circle, or the point of tangency. The slope of the tangent line changes as the point of tangency rotates around the circle.

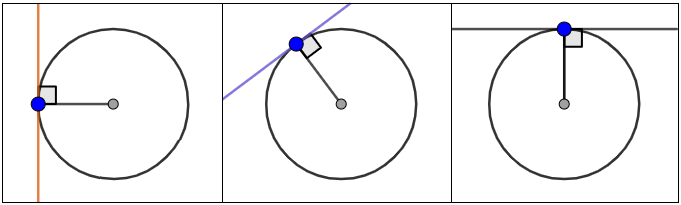
In elementary algebra, slope is defined as the change along the y-axis versus the change along the x-axis. To find the equation of the tangent line given the point of tangency at this level, a typical approach might involve:

• Identifying another point on the radius of the circle that includes the point of tangency, which can be the center of the circle;

• Finding the slope of this radius and then the slope of the perpendicular slope;

• And, using the negative reciprocal and a point to find the equation of the tangent line, which can be done using the point-slope form:

$y - y_1 = m(x - x_1)$

The same concept of tangent line can also be explored through calculus. In fact, a large part of calculus is the study of change, and, more specifically, instantaneous change. Calculus has a wide range of applications ranging from mathematical models representing stock markets to taking rockets to space. Evaluating derivatives in calculus means finding the rate of change, and in the case of a circle, it allows us to find the slope. You may think, "Great, but why do I need another way of finding the slope?" Here is the beauty: the first derivative gives us the equation to find any slope along any smooth curve, not just circles.

Now, consider the circle centered at $(0, 0)$ with a radius of $1$.

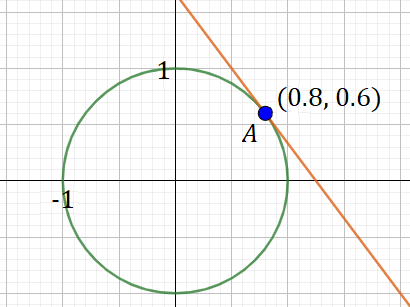
It can be represented via the set of $(x, y)$ points that satisfy the equation,

$x^2 + y^2 =1$

By applying a derivative to both sides of the equation, we easily find out the slope of the tangent line at any point $(x, y)$ on the circle, as long as $y$ is not $0$. For example, the slope of the tangent line at $(0.8, 0.6)$ will be

$-\frac{x}{y} = - \frac{0.8}{0.6} = - \frac{4}{3}$

Then, by using the point-slope formula, we get

$y = - \frac{4}{3} x + \frac{5}{3}$

In fact, the first derivative allows us to easily find the equation of any tangent line to this circle given the point of tangency, again, as long as the $y$-coordinate does not equal $0$. This same tool makes it easy to examine the angle relationships of tangent lines as well.

---

Here is a case where tangent lines of circle appear in geometry. If we build on the previous example and create an additional tangent line, there is an angle at the point where the two tangents intersect.

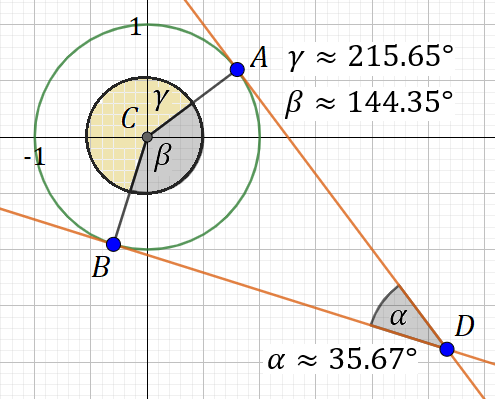
By using trigonometry ratios, we can find the angle of intersecting tangent lines and then use inductive reasoning to infer one of the key theorems in geometry:

The measure of the angle created by the tangent lines is half the difference of the arc measures created by the tangent lines:

\frac{1}{2}\big( m \widearc{AB}_{\text{major}} - m \widearc{AB}_{\text{minor}} \big) = \measuredangle ADB

---

As you grow in your math knowledge, you are not just learning discrete concepts, rather, you are making connections between previously learned concepts. For example, without a firm understanding of slope, the first derivative is meaningless. Mathematics is a subject built from the bottom up, and the seemingly simple concepts learned in elementary mathematics courses are the foundation. The beauty is that as you develop deeper mathematical knowledge, often prior concepts becomes clearer, and you gain a deeper understanding and appreciation of them as well.

In the video below by James Tanton of the Global Math Project, you can explore how geometry can be laced with arithmetic to explore a different approach of finding squares of numbers.

How about you? Have you made connections between concepts taught in different mathematics courses? Did you learn concepts later on in your math education that made earlier concepts clearer? For example, would it be better if we learned about positive and negative numbers through algebra directly? Write to let us know.