Patterns in polygonal numbers

June 23, 2018

Phillip Isaac

Do you have a favourite pattern? In fact, what is the first thing that comes to mind when I ask you that question? I love gardening, and for me, one of the most fascinating things about plants is to see the patterns in how they grow. For example, is the leaf arrangement opposite or alternate? Is the leaf form compound or simple? What colour are the flowers? Identifying such patterns allows us to classify the type of plant, which leads to a better understanding of what grows in our garden. So, what does this have to do with mathematics?

You may have read several of our blog posts that suggest that mathematics is, more or less, the study of patterns (e.g. Seeking Patterns with Math). Such an endeavour can help us to identify and classify different mathematical structures, which ultimately leads us to a deeper understanding of mathematics as an art, a science, and a tool. In this blog post, we look at mathematics relating to polygonal numbers, sometimes also known as figurate numbers.

Let’s start with the triangle. If you draw an equilateral triangle and mark the vertices as dots, there are three dots. Now extend two adjacent edges, and make a bigger triangle. Iterate this process as in the following diagram:

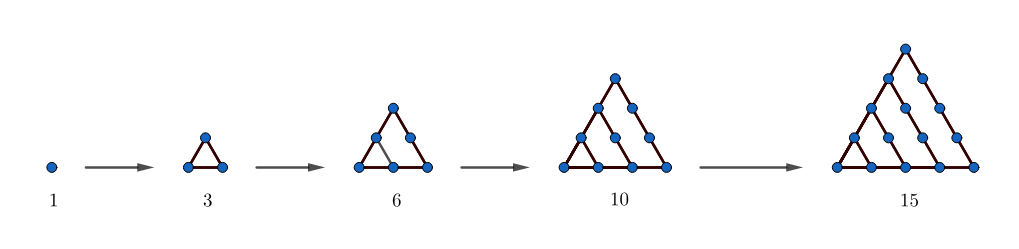
How many dots are there with each iteration? Proceeding in this way, we generate a sequence of positive integers. Note that we start at $1$, which can be thought of as the trivial triangle, i.e. where the shape collapses to a single point. The result is the sequence of the triangular numbers:

$1, 3, 6, 10, 15, 21, 28, 36, 45, \ldots$

Do you notice any patterns in this sequence? One that stands out is the difference of each consecutive number, given by $2, 3, 4, 5, 6, 7, \ldots$ In other words, each of these numbers is the sum of consecutive integers. For example,

$28 = 1 + 2 + 3 + 4 + 5 + 6 + 7.$

Enter Carl Friedrich Gauss. Gauss was a famous German mathematician whose work has made a huge impact on modern mathematics and physics. As a child in the 18th century, he was notoriously precocious. One story, perhaps an urban myth, tells of a frustrated school teacher who instructed a misbehaving Carl Gauss to add all the numbers from $1$ to $100$, in order to keep the child occupied for quite some time. Unfortunately for the teacher, the young Gauss devised the following shortcut.

The sum of the numbers, $T$, can be written in two ways:

$1 + 2 + 3 + \ldots + 98 + 99 + 100 = T,$

$100 + 99 + 98 + \ldots + 3 + 2 + 1 = T.$

Sum up corresponding terms on both sides of each equation to give

$101 + 101 + 101 + \ldots + 101 + 101 + 101 = 2 \times T.$

In the sum on the left, the number $101$ is being added to itself $100$ times. This means the left hand side is just $101 \times 100 = 10100.$ (You may also try Push Ups, Sit Ups and Adding Numbers to think about it!)

Therefore $T = 10100/2 = 5050.$ It turns out this is a triangular number.

In fact, thanks to the young Carl Gauss, we can see that every triangular number can be written in a similar form. Actually, the $n$th triangular number is given by the formula $(n+1)n/2$. Here we are using the typical mathematician’s place holder of "$n$" as an integer variable. For example, if $n=1$, then “$n$th” or “$1$th” is read as “first”. If $n=2$, “$n$th” or “$2$th” is understood as “second”, “$5$th” as fifth, and so on. We then just replace $n$ in the formula for the actual number. Try it:

$28 = (8 \times 7)/2,$

$36 = (9 \times 8)/2,$

and so on.

Here’s an idea: Can we extend this to other regular polygons, like squares, pentagons, hexagons, and so on. The answer is: Yes!

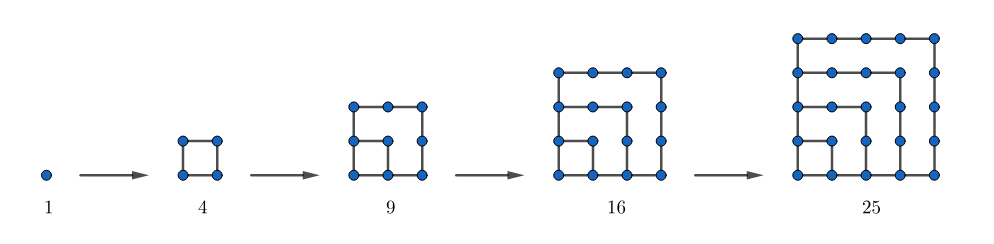
Try applying a similar principle in drawing squares with growing lengths (again, starting at $1$), as we did the triangles. A picture would develop something like this:

The number of dots in each iteration give the square numbers:

$1, 4, 9, 16, 25, 36, 49, 64, \ldots$

In this case, the formula for each number is easy. The $n$th square number is given by $n^2$. What about the differences of consecutive square numbers? These are $3, 5, 7, 9, 11, 13, 15, \ldots$ In other words – and this is cool – the square numbers are the sums of consecutive odd numbers. For example,

$49 = 1 + 3 + 5 + 7 + 9 + 11 + 13.$

Now set the number of sides to $5$. Playing the same game with regular pentagons (that is, five-sided polygons), generating the sequence of numbers might take a bit of effort, concentration, and possibly some artistic talent. Try to follow the progression in the following diagram, and maybe reproduce some more for yourself:

Counting the number of dots in each iteration gives the following sequence:

$1, 5, 12, 22, 35, 51, 70, 92, \ldots$

These are known as the pentagonal numbers. What is the pattern here? The differences of consecutive pentagonal numbers are $4, 7, 10, 13, 16, 19, 22, \ldots$ So, for example, the pentagonal numbers are the sums of consecutive number, starting at $1$, that differ by $3$. For example:

$70 = 1 + 4 + 7 + 10 + 13 + 16 + 19.$

What about a formula for the $n$th pentagonal number? We could use the same principle put forward by Gauss. The $n$th pentagonal number, $P$, can be written as

$1 + 4 + 7 + \ldots + (3n-8) + (3n-5) + (3n-2) = P,$

$(3n-2) + (3n-5) + (3n-8) + \ldots + 7 + 4 + 1 = P.$

As we did with the triangular numbers, sum up corresponding terms on both sides of each equation to give

$(3n-1) + (3n-1) + (3n-1) + \ldots + (3n-1) + (3n-1) + ( 3n-1) = 2P$

In the sum on the left, the number $(3n-1)$ is being added to itself $n$ times. This means the left hand side is just $(3n-1)n.$ Therefore $P = (3n-1)n/2.$ Try some examples:

$70 = (3 \times 7 -1) \times 7/2,$

$92 = (3 \times 8 -1) \times 8/2,$

and so on.

It is at this point, we can say “AHA! There is a pattern!” Consecutive triangular numbers have a difference of whole numbers (that differ by $1$). Consecutive square numbers have a difference of odd numbers (that differ by $2$). Now we see that consecutive pentagonal numbers have a difference of a sequence of numbers that differ by $3$. Could it be that this pattern extends to numbers associated with hexagons ($6$-sided), heptagons ($7$-sided), octagons ($8$-sided), and so on? Indeed, that is the case.

If you can, try to verify some of the following results by drawing pictures of growing hexagons, heptagons, octagons, and by extrapolating. The result is the following table of numbers, with $p$ being the number of sides of the polygon:

$n$	$p=3$	$p=4$	$p=5$	$p=6$	$p=7$	$p=8$	$p=9$	$p=10$	$p=11$	$p=12$
1	1	1	1	1	1	1	1	1	1	1
2	3	4	5	6	7	8	9	10	11	12
3	6	9	12	15	18	21	24	27	30	33
4	10	16	22	28	34	40	46	52	58	64
5	15	25	35	45	55	65	75	85	95	105
6	21	36	51	66	81	96	111	126	141	156
7	28	49	70	91	112	133	154	175	196	217
8	36	64	92	120	148	176	204	232	260	288
9	45	81	117	153	189	225	261	297	333	369
10	55	100	145	190	235	280	325	370	415	460
11	66	121	176	231	286	341	396	451	506	561
12	78	144	210	276	342	408	474	540	606	672

Here is where you can let your inner mathematician roam free. What patterns do you notice in this table? How about the differences across each row? Are there any interesting patterns down diagonal entries? Could you apply the Gauss idea to find a formula for the $n$th entry in each column? (We have already worked out a formula for columns $p=3$, $p=4$ and $p=5$).

Could you work out a formula for arbitrary $p$? Here is the big challenge: Is it possible to reproduce a similar table for number sequences related to three-dimensional polyhedra? Are there any restrictions on the numbers of edges or faces in this case?

I hope you enjoy playing with these patterns. Happy exploring!